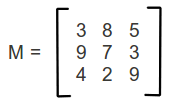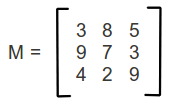Fonte: Walter Marlon Mamedes Avila

---

1. 5.0 Vetores e Matrizes em algoritmos
2. Vetores
3. Matrizes
4. Material Extra

Na aula, você aprenderá manipular grandes conjuntos de dados com os arrays, ou seja, você verá como pode manipular várias variáveis como se fossem uma única.

Vetores

A abstração para um vetor pode ser entendida como um conjunto de variáveis do mesmo tipo acessíveis com um único nome, armazenadas de forma contínua e ocupando as posições (índices) de forma fixas. Pode-se também dizer, de maneira geral, que vetor é uma matriz unidimensional.

Exemplo: Considere uma sala de aula, onde há 10 alunos e queremos armazenar suas idades em variáveis, até então seria feito assim:

DECLARE idade1, idade2, idade3, idade4, idade5, idade6, idade7, idade8, idade9, idade10 INTEIRO;

Como sabemos, podemos inicializar uma variável de duas formas:

idade1= 10, idade2 = 12, idade3 = 11 … idade10 =10;

Ou pedir que o usuário escreva usando o teclado:

Escreva (“Digite a idade do primeiro aluno”)
Leia (aluno1)
Escreva (“Digite a idade do segundo aluno”)
Leia (aluno2)
…

Não foi tão difícil criar uma variável que armazena a idade de cada aluno, porém, se formos fazer diversos cálculos com as idades ou ainda considerar uma sala com 1000 alunos, já ficaria muito mais difícil.

O vetor é uma estrutura que simplifica essas operações com variável do mesmo tipo, considerando que toda idade é do tipo inteiro, criamos um vetor de 10 posições para seguir o mesmo exemplo usado à cima.

idade:vetor[1..10] de inteiro

Na declaração usamos o tamanho máximo que o vetor pode ter, podendo usar o tamanho total declarado ou menos.

Para acessar a idade do primeiro aluno: idade[1]
Para acessar a idade do segundo aluno: idade[2]
…
Para acessar a idade do décimo aluno: idade[10]

Para atribuir valores para os vetores, usamos o operador `<-` e fornecemos o valor para cada posição:

idade[1] <- 26;
idade[2] <- 17;
 …
idade[10] <- 19;

O trecho de pseudocódigo acima mostra exemplifica que serão armazenadas todas as idades dos respectivos alunos e assim poderão ser acessadas separadamente.

Um questionamento: “é quase a mesma dificuldade para acessar em comparação à estrutura simples?”. Sim, dessa forma foi, porém será mostrado agora algo bem característico da estrutura vetorial que simplifica as operações com a variável.

São usadas duas variáveis do tipo inteiro para auxiliar na inserção de elementos dentro do vetor. Vou considerar aqui a variável n que armazenará o tamanho que meu vetor tiver, e a variável i que será usada com o auxílio da estrutura de repetição para ou for que acessará cada variável de forma mais fácil e rápida como demonstrado à baixo.

algoritmo "vetor"
var
n:inteiro
j:inteiro
valor:inteiro
idade:vetor[1..10] de inteiro

inicio
Escreva("Digite a quantidade de alunos na sala")
Leia(n)

para i de 1 ate n faca
 leia(valor)
 aluno[i] <- valor
fimpara

fimalgoritmo

Usando a variável idade[3] onde i=3, poderemos acessar a idade do 3° aluno, a variável idade[2] onde i=2, acessará a idade do 2° alunos, e assim sucessivamente para todos os outros.

Vejamos um exemplo comparativo: Considere o fato de que precisamos fazer uma média de idade de todos os alunos dentro de uma sala de aula e considerando que todas as 10 variáveis já tenham sido inicializadas com as idades dos respectivos alunos.

Usando as variáveis de tipo simples teríamos o seguinte pseudocódigo

DECLARE media NUMERICO; // Essa variável armazenará valores numéricos
media <-  media +(idade1,idade2,idade3,idade4,idade5, idade6, idade7, idade8, idade9, idade10)/10;

Usando as variáveis de tipo vetor teríamos o seguinte pseudocódigo:

media<- 0; // a variável media precisa ser inicializa com zero

Para i=1; i<=n ; i++ faça // percorrendo todas as idades dos n alunos.

  media<- media +idade[i]; // aqui será somente a soma de todas as idades
Fimpara

media<-media/n ; // aqui será de fato calculado e media.

Como visto até agora, vetores são uma estrutura que simplifica as operações com variáveis do mesmo tipo, trazendo um novo conceito que é bastante usado em quase todos os programas.

Matrizes

À base da estrutura vetorial, com a diferença de ser n-dimensional, a matrizes tem suas peculiaridades.

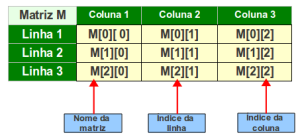
Inserção: Assim como o vetor, usamos variáveis auxiliares, porém em matrizes usaremos duas a mais, aqui a variável linhas armazenará o número de linhas que a matriz tiver, a variável colunas armazenara a quantidade de colunas que a matriz tiver, e as variáveis i e j que dentro da estrutura de repetição aqui usada para ou for para percorrer ou acessar todas as posições.

algoritmo "vetor_matriz"
var
linhas:inteiro
colunas:inteiro
i:inteiro
j:inteiro
valor:inteiro
matriz:vetor[1..3,1..3] de inteiro

inicio

para i de 1 ate 3 faca
  escreval("Informe os dados da linha ",i)
  para j de 1 ate 3 faca
    escreval("Informe os dados da coluna ",j)
    leia(valor)
    matriz[i,j] <- valor
  fimpara
fimpara

i <- 1
j <- 1
para i de 1 ate 3 faca
  para j de 1 ate 3 faca
    escreva(matriz[i,j])
  fimpara
fimpara
fimalgoritmo

Como mostrado na imagem acima, todas as posições possíveis de uma matriz 3×3.

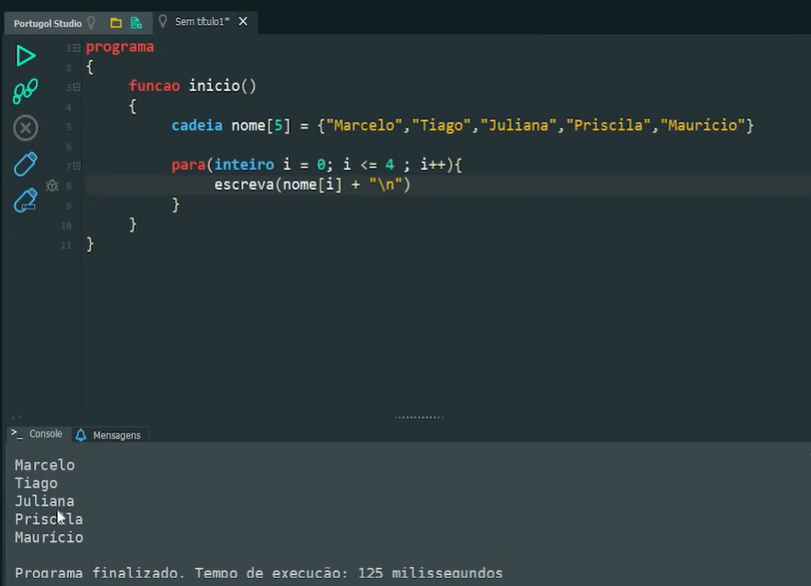
Em algoritmos, embora possamos iniciar pelo 1, é padrão que os índices dos vetores e matrizes iniciem pelo 0. Veja a figura do pseudocódigo a seguir

---

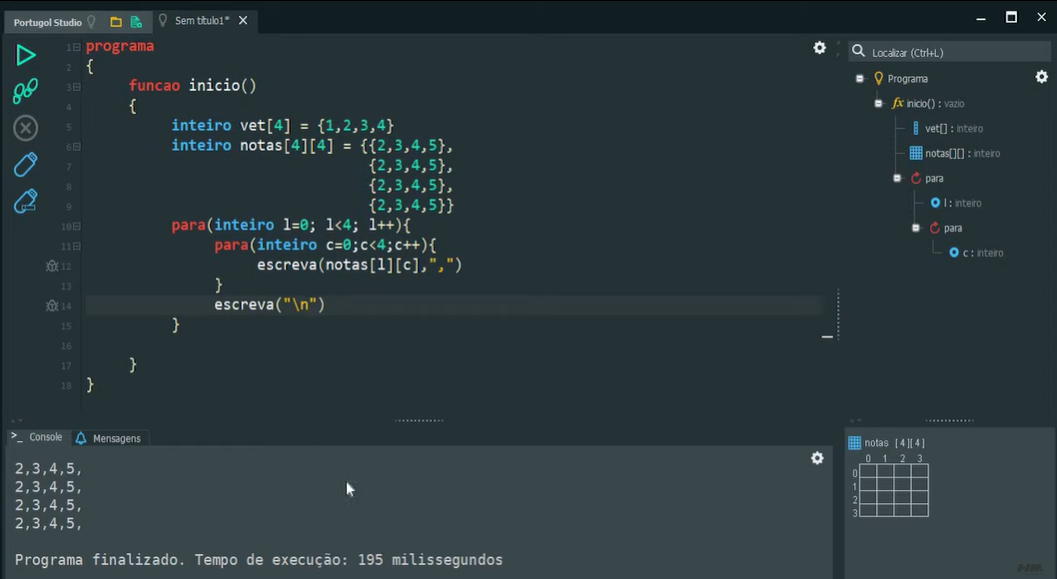
Traga suas perguntas e dúvidas para o fórum e compartilhe com seus colegas ou verifique na seção perguntas e respostas se sua pergunta já não se encontra respondida lá.

O que você aprendeu:

– Vetores
– Matrizes