Gráficos – Resistor Ôhmico

Adaptado do original: Prof Roberto Rech

Qual dos gráficos a seguir pode representar a resistência (\(R \)), em função da secção transversal (\(S\)), de um fio condutor ôhmico de comprimento constante?

1ª Lei de Ohm – estabelece que um resistor pode ser dito ôhmico quando for constante a razão entre a diferença de potencial (ddp) ou tensão a que é submetido e a intensidade de corrente elétrica que o percorre.

2ª Lei de Ohm – estabelece a relação entre a resistência, o material do qual o resistor é construído e sua geometria, em geral as dimensões (comprimento e área de secção transversal)

Em termos de expressão:

\(R = \rho \frac{l}{S} \)

em que:

\(R \) = resistência elétrica
\(rho \) = resistividade  (constante)
\(l\) = comprimento do condutor (constante para o caso apresentado)
\(S \) = área da secção transversal.

Para o problema apresentado, a resistência elétrica varia de acordo com a variação da área da secção transversal do condutor.
A função que relaciona \(R \) e \(S\) é uma função racional do tipo \(R = f(S) \), pois o produto da resistividade pelo comprimento é constante. Portanto \(R \) é inversamente proporcional à área da secção transversal \(S \) do condutor.  Quando a variável independente está localizada no denominador, a função é dita racional. O gráfico de uma função racional é uma hipérbole equilátera, veja um exemplo da função \(y = 1 / x \), pense em \(y\) como \(R\) e \(x\) como \(S \):

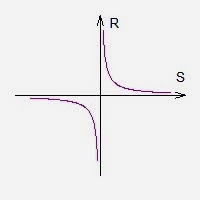
Como a área é sempre um número positivo, vale apenas a assíntota (cada uma das partes da hipérbole equilátera) do primeiro quadrante, portanto a resposta correta está representada no gráfico da letra (c).

—